The Math of Idle Games, Part I

Originally published October 4, 2016

I’ve given a few talks in the past about the appeal and general mechanics of idle games, but what if you actually wanted to make one? Theory and patterns are nice, but there’s some complicated math running behind it. And how on earth do you balance a game that has insanely large numbers?

This article is Part I of what will be a three-part series detailing topics covered in my most-recent talk. Part I discusses core ideas of growth, cost, prestige, and generator balancing. Part II will look into alternate growth methods (especially derivative-based). Part III will look at prestige cycles and balance.

The models for all of the charts produced in these articles are available as spreadsheets. Please feel free to duplicate, peruse, experiment, extend, etc.!

Let’s start by specifying some terminology to make talking about this easier.

• Primary Currency: This is the main number that is being incremented, generally the goal of the game. Usually it’s some form of money.
• Generator: The items in the game that produce primary currency. The rate of production, or income, is measured as currency per second.
• Primary Exchange Currency: In some cases generators produce a different currency that is exchanged for primary currency. For example, in Clicker Heroes the generators produce DPS, which is then converted into gold by killing monsters. That layer of separation can give you a bit more control over the growth of the primary currency in the game, since you can modify the “exchange rate” over time.
• Multiplier: Any of a variety of upgrades that multiplies your generator power. These can be explicit upgrades, based on number of generators owned, etc. Their purpose is to (temporarily) get production closer to, or ahead of, costs.
• Prestige: A reset of most elements of the game (especially generators and multipliers), but gaining currency (prestige currency) and/or persistent multipliers to accelerate the next time through. Similar to a “New Game+”.

At the most basic level, idle games are a seesaw between production rates and costs. Early on in a run, your production will exceed costs while eventually costs will become prohibitive. This is typically accomplished by having costs grow exponentially while production grows at a linear or polynomial rate. To put that into formulas:

$cost_{next} = cost_{base} \times (rate_{growth})^{owned}$

$production_{total} = (production_{base} \times owned) \times multipliers$

With AdVenture Capitalist Lemonade Stands, the $rate_{growth} = 1.07$, $cost_{base} = 4^*$, and $production_{base} = 1.67/sec$. So if you own 10 Lemonade Stands:

$cost_{next} = 4 \times (1.07)^{10} = 7.87$

Meanwhile, the production rate is:

$production_{total} = (1.67 \times 10) \times 1 = 16.7 / sec$

$^*$It’s technically 3.738, since you get the first one for free and it’s actually the second one that costs 4.

Here are the actual values for AdVenture Capitalist (thank you AdCap wiki!):

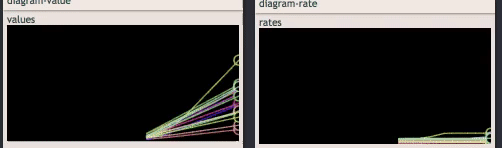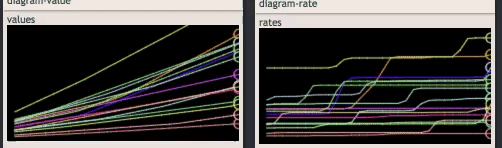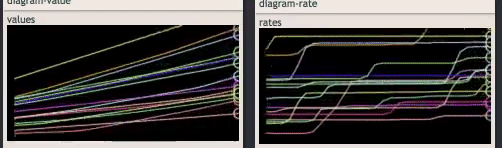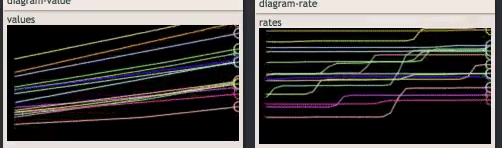
So early on you’re earning well beyond the cost of a new generator every second. Let’s look at that in graph form. Note that when you own 25 and 50 Lemonade Stands, the rate gets a (stacking) x2 multiplier.

And we can see a slightly bigger picture if we use a log scale y-axis.

Early on, your production rate is high and you can keep buying, and the multipliers bump you back up whenever it gets close. But eventually the costs become overwhelming, and the time you would have to wait to be able to afford the next generator gets prohibitively long.

Mathematically, exponential growth (anything of the form $n^x$, for $n > 1$) will eventually catch and far exceed any polynomial growth ($x^k$) no matter how big $k$ is or how small $n$ is. This can take a very long time in some cases, but that’s where balancing comes in. (If you want a great overview about tiers of quickly-growing functions, check out this post by Eclipse1agg, the developer of True Exponential.)

In this example, once things really start to slow down, you would be looking to do a prestige to multiply your production rate. Doing that looks like this, with each successive prestige sliding up on the graph. The result is that each prestige allows the player to get farther through the cost curve before falling behind.

But that’s for a single generator. What happens when you have multiple generators, each with different costs and rates? Now the player has choices about what to invest in, and things get more complicated. Fortunately, we can model optimal behavior too! In this model we define “optimal” as having the best income:cost ratio, and we determine that at every purchase opportunity.

Players aren’t going to follow this exactly because the optimal choice will often be far too micromanage-y for a human. "Buy one Generator 2, then three Generator 1s, then a Generator 3, then another Generator 1," etc. Instead, players usually buy in bulk to simplify the decision process...or to be super OCD (always keeping at multiples of 100). But over the long run, players will roughly be in this ballpark.

Here’s what it looks like for the first 5 generators in AdVenture Capitalist, with x2 multipliers kicking in when you own 25 and 50 of a generator. You can see the expected spikes in purchases right around 25 and 50 multipliers kicking in, since those are temporarily overvalued. Note: this model simplifies income to be per-second instead of requiring a timer to complete, so higher-end, slower generators get over-favored.

If we look at a log scale of income rates, though, you’ll notice that the newest generator is nearly always dominant once it can be purchased. That’s not very interesting for the player, though. It means that older generators are largely irrelevant and removes any interesting decisions. Even if smaller generators are technically “optimal,” they may not matter. For example, it may be that you can buy a lemonade stand that generates 10 currency/sec for 5 currency or a car wash that generates 10,000 currency/sec for 7,500 currency. Lemonade is a better deal, but as a player you’re not going to “feel” the impact and so it doesn’t seem worth purchasing, or perhaps more accurately not worth the effort to consider purchasing.

However, even with a simple model like this one, we can start to emulate the shifting priorities of the various generators. In the above image we don’t have any purchasable multiplier upgrades, and every generator gets the same multiplier count bonuses shown in the table below (only Gen 1 hits 100):

If we modify these numbers and keep everything else the same (including still not having any purchasable upgrades), we can create a very different picture. We’ll use these multiplier values instead:

And here’s the resulting income graph:

Now that’s much more interesting! As you progress through the game, different generators take priority and have the biggest impact on income. The player gets to try to identify these priorities (they won’t always be obvious right away), and this provides more variety and less predictability. And if you have purchasable upgrades, you have even more options for providing this sort of variation for the players.

BONUS CONTENT!

While putting all this together, I derived two very useful formulas that will save you from brute-forcing with some lengthy for-loops. The first will calculate the cost of bulk-buying generators, the second will calculate the max generators you can buy with your current funds. These will only work for simple exponential growth that doesn't have shifting costs or exponents, so make sure your particular application works for it. For both of these, the variables are:

$n$ = the number of generators to buy
$b$ = the base price
$r$ = the price growth rate exponent
$k$ = the number of generators currently owned
$c$ = the amount of currency owned

$cost = b * \frac{r^k(r^n-1)}{r-1}$

$max = floor(log_r(\frac{c(r-1)}{b(r^k)}+1))$

Or, if your language can't do a non-standard $log$ base, you can use a standard $log$ or $ln$ and divide it like this:

$max = floor(\frac{log(\frac{c(r-1)}{b(r^k)}+1)}{log(r)})$

(For those who are curious, all formulas in this post were created dynamically with an embedded script called Mathjax that lets you render LaTeX or MathML very easily and cleanly.)

If you have questions, find a bug, decide to make an extension to a sheet, or have an awesome new idle game you want to share, please feel free to reach out and email me at anthony.pecorella@leveluplabs.com.